2016-10-10

TensorFlowで学ぶディープラーニング入門備忘録【第２章】

TensorFlowで学ぶディープラーニング入門 ~畳み込みニューラルネットワーク徹底解説~

作者: 中井悦司
出版社/メーカー: マイナビ出版
発売日: 2016/09/27
メディア: 単行本（ソフトカバー）
この商品を含むブログを見る

第１章からの続きになる。

2.1　ロジスティック回帰による二項分類器

2.1.1　確率を用いた誤差の評価

第１章でも論じた、与えられたデータをウイルスに感染している・していないに分類する二項分類器（パーセプトロン）のモデルを取り上げる。ただし、単純に２種類に分類するのではなく、確率を用いてすすめる。第１章でも論じたように、検査結果(x1,x2)に対して、ウイルスに感染している確率は、

${ \displaystyle \begin{equation} P(x_1,x_2)=\sigma(f(x_1,x_2)) \tag{2.3} \end{equation} }$

で表される。ここで、仮にパラメータw0,w1,w2が具体的に決まっているとして、最初に与えられたデータを改めて予測し直してみる。まず、与えられたデータは全部でN個あるものとして、n番目のデータを(x1n,x2n)とする。またデータが実際に感染している場合、tn=1、感染していない場合、tn=0とする。n番目のデータが感染している確率はP(x1n,x2n)で与えられるので、この確率に応じて感染していると予測する。0〜1の間で乱数を発生させて、P(x1n,x2n)以下であれば感染している、と予測することにする。

この方法で予測した場合、正解する確率はどれほどだろうか。tn=1のとき、つまり実際に感染しているときに感染していると予測する確率はP(x1n,x2n)そのものなので、これが正解する確率に一致する。一方、tn=0、つまり実際には感染していない場合、感染していないと正しく予測する確率は1-P(x1n,x2n)になる。これは、以下の数式で一度に書ける。

${ \displaystyle \begin{equation} P_n = \{P(x_{1n},x_{2n})\}^{t_n}\{1-P(x_{1n},x_{2n})\}^{1-t_n} \tag{2.4} \end{equation} }$

そしてN個のデータ全てに正解する確率Pは、個々のデータを正解する確率の掛け算で計算することができ、

${ \displaystyle \begin{equation} P=P_1 \times P_2 \times \cdot \cdot \cdot \times P_N = \prod_{n=1}^{N}P_N \tag{2.5} \end{equation} }$

あるいは、

${ \displaystyle \begin{equation} P = \prod_{n=1}^{N} \{P(x_{1n},x_{2n})\}^{t_n}\{1-P(x_{1n},x_{2n})\}^{1-t_n} \tag{2.6} \end{equation} }$

と書ける。この確率がパラメータw0,w1,w2を評価する基準になる。このように「与えられたデータを正しく予測する確率を最大化する」手法は最尤(さいゆう)推定法と呼ばれる。これでパラメータの良し悪しを判断する基準、すなわち「機械学習モデルの３ステップ」のステップ２が用意できた。TensorFlowで計算する場合、式(2.6)のような掛け算を大量に含む演算は効率が良くないので、次式で誤差関数Eを定義する。

${ \displaystyle \begin{equation} E = -\log P \tag{2.7} \end{equation} }$

これでPを最大にすることと、-logPを最小にすることが同値になった。 (2.6)を(2.7)に代入し、変形すると、誤差関数Eは

${ \displaystyle \begin{equation} E = -\log \prod_{n=1}^{N} \{P(x_{1n},x_{2n})\}^{t_n}\{1-P(x_{1n},x_{2n})\}^{1-t_n} \\ = - \sum_{n=1}^{N}[t_n \log P(x_{1n},x_{2n})+(1-t_n) \log \{ 1-P((x_{1n},x_{2n}) \} ] \tag{2.9} \end{equation} }$

と表される。

2.1.2　TensorFlowによる最尤推定の実施

TensorFlowでこれまでの数式を表現する。まずはモジュールのインポートを以下で行う。

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from numpy.random import multivariate_normal, permutation
import pandas as pd
from pandas import DataFrame, Series

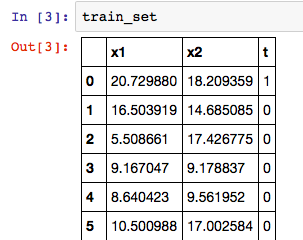
次に行うのが、トレーニングセットのデータの用意だ。

#乱数のシードを決める。20160512という数字に意味はない。同じ数字を指定すると、毎回同じデータが生成される。
np.random.seed(20160512)

#t=0(非感染)のデータを乱数で発生
n0, mu0, variance0 = 20, [10, 11], 20
data0 = multivariate_normal(mu0, np.eye(2)*variance0 ,n0)
df0 = DataFrame(data0, columns=['x1','x2'])
df0['t'] = 0

#t=1(感染)のデータを乱数で発生
n1, mu1, variance1 = 15, [18, 20], 22
data1 = multivariate_normal(mu1, np.eye(2)*variance1 ,n1)
df1 = DataFrame(data1, columns=['x1','x2'])
df1['t'] = 1

#データを一つにまとめ、行の順番をランダムに入れ替え
df = pd.concat([df0, df1], ignore_index=True)
train_set = df.reindex(permutation(df.index)).reset_index(drop=True)

これで、データセットが整った。Jupyterのノートブック上で、データフレームの内容は以下コマンドから表で確認できる。

train_set

f:id:tosh419:20161010165136p:plain

ただしTensorFlowで計算する際は各種のデータを多次元配列で表現する必要があった。そこで、(x1n,x2n)とtnをn=1〜Nについて縦に並べた行列を次のように定義する。

${ \displaystyle \begin{equation} X=\begin{pmatrix} x_{11} & x_{21} \\ x_{12} & x_{22} \\ x_{13} & x_{23} \\ . & . \\ . & . \\ . & . \end{pmatrix}, t=\begin{pmatrix} t_1 \\ t_2 \\ t_3 \\ . \\ . \\ . \end{pmatrix} \tag{2.10} \end{equation} }$

トレーニングセットに含まれるそれぞれのデータを(2.1)のf(x1,x2)に代入した結果は次のように表現できる。

${ \displaystyle \begin{equation} \begin{pmatrix} f_1 \\ f_2 \\ f_3 \\ . \\ . \\ . \end{pmatrix} = \begin{pmatrix} x_{11} & x_{21} \\ x_{12} & x_{22} \\ x_{13} & x_{23} \\ . & . \\ . & . \\ . & . \end{pmatrix} \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} + \begin{pmatrix} w_0 \\ w_0 \\ w_0 \\ . \\ . \\ . \end{pmatrix} \tag{2.11} \end{equation} }$

これをさらにシグモイド関数に代入したものが、n番目のデータがt=1である確率Pnになる。

${ \displaystyle \begin{equation} \begin{pmatrix} P_1 \\ P_2 \\ P_3 \\ . \\ . \\ . \end{pmatrix} = \begin{pmatrix} \sigma (f_1) \\ \sigma (f_2) \\ \sigma (f_3) \\ . \\ . \\ . \end{pmatrix} \tag{2.12} \end{equation} }$

ここまでをTensorFlowのコードで表現する。

#train_setに対応するデータをarrayオブジェクトとして変数train_xとtrain_tに格納する
train_x = train_set[['x1','x2']].as_matrix()
train_t = train_set['t'].as_matrix().reshape([len(train_set), 1])
#
x = tf.placeholder(tf.float32, [None, 2])
w = tf.Variable(tf.zeros([2, 1]))
w0 = tf.Variable(tf.zeros([1]))
#tf.matmul(x,w)とw0は本来足し合わせられないが、下述のブロードキャストルールが適用される。
f = tf.matmul(x, w) + w0
p = tf.sigmoid(f)

TensorFlowのリスト演算における特別なルールで、多次元リストに１要素からなる値を足した場合、リストの各要素に同じ値が足される。

・行列とスカラーの足し算は、各成分に対する足し算になる

${ \displaystyle \begin{equation} \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} + (10) = \begin{pmatrix} 11 & 12 & 13 \\ 14 & 15 & 16 \\ 17 & 18 & 19 \end{pmatrix} \end{equation} }$

・同じサイズの行列の*演算は、成分ごとの掛け算になる

${ \displaystyle \begin{equation} \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} * \begin{pmatrix} 10 & 100 & 1000 \\ 10 & 100 & 1000 \\ 10 & 100 & 1000 \end{pmatrix} = \begin{pmatrix} 10 & 200 & 3000 \\ 40 & 500 & 6000 \\ 70 & 800 & 9000 \end{pmatrix} \end{equation} }$

・スカラーを受け取る関数を行列に適用すると、各成分に関数が適用される

${ \displaystyle \begin{equation} \sigma \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} \sigma (1) \\ \sigma (2) \\ \sigma (3) \end{pmatrix} \end{equation} }$

続いて、誤差関数をTensorFlowのコードで表現し、これを最小化するためのトレーニングアルゴリズムを指定する。これは、式(2.9)で与えられており、次のようになる。

t = tf.placeholder(tf.float32, [None, 1])
loss = -tf.reduce_sum(t*tf.log(p) + (1-t)*tf.log(1-p))
train_step = tf.train.AdamOptimizer().minimize(loss)

さらに、正解率を表す計算値を定義する。仮に、n番目のデータに対して、Pn>0.5であればt=1、そうでなければt=0とし、正解率がいくらになるかを計算する。

#(Pn-0.5)と(tn-0.5)の符号を比較し、予測が正解かを判定。signは符号を取り出す関数。
correct_prediction = tf.equal(tf.sign(p-0.5), tf.sign(t-0.5))
#tf.cast関数でbooleanを1,0に変換し、全体の平均値を計算する。
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

実際の最適化に入る。

#セッションを用意し、Variableの値を初期化
sess = tf.Session()
sess.run(tf.initialize_all_variables())
#勾配降下法による最適化を20000回繰り返す。
i = 0
for _ in range(20000):
    i += 1
    sess.run(train_step, feed_dict={x:train_x, t:train_t})
    if i % 2000 == 0:
        loss_val, acc_val = sess.run(
            [loss, accuracy], feed_dict={x:train_x, t:train_t})
        print ('Step: %d, Loss: %f, Accuracy: %f'
               % (i, loss_val, acc_val))

これを行うと、誤差関数lossと正解率accuracyの値が表示される。

Step: 2000, Loss: 15.165894, Accuracy: 0.885714
Step: 4000, Loss: 10.772635, Accuracy: 0.914286
Step: 6000, Loss: 8.197757, Accuracy: 0.971429
Step: 8000, Loss: 6.576121, Accuracy: 0.971429
Step: 10000, Loss: 5.511973, Accuracy: 0.942857
Step: 12000, Loss: 4.798011, Accuracy: 0.942857
Step: 14000, Loss: 4.314180, Accuracy: 0.942857
Step: 16000, Loss: 3.986264, Accuracy: 0.942857
Step: 18000, Loss: 3.766511, Accuracy: 0.942857
Step: 20000, Loss: 3.623064, Accuracy: 0.942857

最適化を打ち切り、この時点でのパラメータの値を取得する。

w0_val, w_val = sess.run([w0, w])
w0_val, w1_val, w2_val = w0_val[0], w_val[0][0], w_val[1][0]
print w0_val, w1_val, w2_val

最後に、取り出した値を用いて、結果をグラフに表示する。

train_set0 = train_set[train_set['t']==0]
train_set1 = train_set[train_set['t']==1]

fig = plt.figure(figsize=(6,6))
subplot = fig.add_subplot(1,1,1)
subplot.set_ylim([0,30])
subplot.set_xlim([0,30])
subplot.scatter(train_set1.x1, train_set1.x2, marker='x')
subplot.scatter(train_set0.x1, train_set0.x2, marker='o')

linex = np.linspace(0,30,10)
liney = - (w1_val*linex/w2_val + w0_val/w2_val)
subplot.plot(linex, liney)

field = [[(1 / (1 + np.exp(-(w0_val + w1_val*x1 + w2_val*x2))))
          for x1 in np.linspace(0,30,100)]
         for x2 in np.linspace(0,30,100)]
subplot.imshow(field, origin='lower', extent=(0,30,0,30),
               cmap=plt.cm.gray_r, alpha=0.5)

f:id:tosh419:20161010181121p:plain

ここでは、グラフ上の色の濃淡が確率P(x1,x2)の値の大きさに対応しており、シグモイド関数が表現されていることが分かる。シグモイド関数

${ \displaystyle \begin{equation} \frac{1}{1 + e^{-x}} \end{equation} }$

はロジスティック関数とも呼ばれており、ここで用いた分析手法はロジスティック回帰と呼ばれる。

2.1.3　テストセットを用いた検証

ここまでで、与えられたデータを正確に予想することを行ってきたが、本来の目的は未知のデータに対して予測の精度を上げることである。特にトレーニングセット(学習用データ)に対する正解率が非常に高いのにも関わらず、未知のデータに対する予測精度はあまり良くない現象を過学習もしくはオーバーフィッティングと呼ぶ。これを避けるためによく行われるのが、あえて一部のデータをテスト用に取り分ける方法だ。例えば、80%のデータで学習を行いながら、残りの20%のデータに対する正解率の変化を見ていくのだ。

そこで、これから今までのコードを修正し、トレーニングセットとテストセットのそれぞれに対する正解率の変化を確認する。

まず、乱数でデータを作成したあと、80%をトレーニングセットのデータ用、20%をテストセットのデータとして取り分ける。

#インポートと乱数シードの設定
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from numpy.random import multivariate_normal, permutation
import pandas as pd
from pandas import DataFrame, Series

np.random.seed(20160531)

#80%をトレーニング用、20%をテスト用として取り分け
n0, mu0, variance0 = 800, [10, 11], 20
data0 = multivariate_normal(mu0, np.eye(2)*variance0 ,n0)
df0 = DataFrame(data0, columns=['x','y'])
df0['t'] = 0

n1, mu1, variance1 = 600, [18, 20], 22
data1 = multivariate_normal(mu1, np.eye(2)*variance1 ,n1)
df1 = DataFrame(data1, columns=['x','y'])
df1['t'] = 1

df = pd.concat([df0, df1], ignore_index=True)
df = df.reindex(permutation(df.index)).reset_index(drop=True)

num_data = int(len(df)*0.8)
train_set = df[:num_data]
test_set = df[num_data:]

#トレーニングセット用、テスト用の変数に格納
train_x = train_set[['x','y']].as_matrix()
train_t = train_set['t'].as_matrix().reshape([len(train_set), 1])
test_x = test_set[['x','y']].as_matrix()
test_t = test_set['t'].as_matrix().reshape([len(test_set), 1])

#各種計算式定義
x = tf.placeholder(tf.float32, [None, 2])
w = tf.Variable(tf.zeros([2, 1]))
w0 = tf.Variable(tf.zeros([1]))
f = tf.matmul(x, w) + w0
p = tf.sigmoid(f)

t = tf.placeholder(tf.float32, [None, 1])
loss = -tf.reduce_sum(t*tf.log(p) + (1-t)*tf.log(1-p))
train_step = tf.train.AdamOptimizer().minimize(loss)

correct_prediction = tf.equal(tf.sign(p-0.5), tf.sign(t-0.5))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

#セッションを用意
sess = tf.Session()
sess.run(tf.initialize_all_variables())

#勾配降下法を繰り返し、トレーニングセットとテストセットに対する正解率の変化を記録
train_accuracy = []
test_accuracy = []
for _ in range(2500):
    sess.run(train_step, feed_dict={x:train_x, t:train_t})
    acc_val = sess.run(accuracy, feed_dict={x:train_x, t:train_t})
    train_accuracy.append(acc_val)
    acc_val = sess.run(accuracy, feed_dict={x:test_x, t:test_t})
    test_accuracy.append(acc_val)

#結果をグラフに表示する
fig = plt.figure(figsize=(8,6))
subplot = fig.add_subplot(1,1,1)
subplot.plot(range(len(train_accuracy)), train_accuracy,
             linewidth=2, label='Training set')
subplot.plot(range(len(test_accuracy)), test_accuracy,
             linewidth=2, label='Test set')
subplot.legend(loc='upper left')

f:id:tosh419:20161010190227p:plain

上図を見ると、勾配降下法の試行回数に従い正解率が上昇していることが分かるが、トレーニングセットとテストセットで正解率が一致していないことが分かる。オーバーフィッティングが発生した場合、トレーニングセットよりも先に、テストセットに対する正解率が増加しなくなる。

2.2　ソフトマックス関数と多項分類器

2.1ではロジスティック回帰を用いて、平面上のデータを２種類に分類する二項分類器（パーセプトロン）を試した。ここからは、データを３種類以上に分類する多項分類器と分類結果を確率で表現するソフトマックス関数を取り扱う。

2.2.1　線形多項分類器の仕組み

はじめに、(x1,x2)平面を３つの領域に分割することを考える。

２分割のときf(x1,x2)=0なる関数で定義する直線が平面を２分割できた。z軸を加えると、z=0で決まる平面で、(x1,x2)平面が上下に２分割される事がわかる。ここで、次の３つの関数を用意し、それを３次元空間に描くことを考えると、異なる方向に傾いた２平面は１本の直線で交わり、３平面は１点で交わることが分かる。結果、どの平面が一番上になっているかで、(x1,x2)平面を３領域に分割することが可能になる。

${ \displaystyle \begin{equation} f_1(x_1,x_2)=w_{01}+w_{11}x_1+w_{21}x_2 \tag{2.13} \end{equation} }$

${ \displaystyle \begin{equation} f_2(x_1,x_2)=w_{02}+w_{12}x_1+w_{22}x_2 \tag{2.14} \end{equation} }$

${ \displaystyle \begin{equation} f_2(x_1,x_2)=w_{03}+w_{13}x_1+w_{23}x_2 \tag{2.15} \end{equation} }$

３つの平面が交わる点(x1,x2)は

${ \displaystyle \begin{eqnarray} \begin{cases} f_1(x_1,x_2)=f_2(x_1,x_2) & \\ f_2(x_1,x_2)=f_3(x_1,x_2) & \tag{2.17} \end{cases} \end{eqnarray} }$

の解となる点で、行列式を用いて、

${ \displaystyle \begin{equation} M \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = w \tag{2.18} \end{equation} }$

ただし、

${ \displaystyle \begin{equation} M = \begin{pmatrix} w_{11} - w_{12} & w_{21} - w_{22} \\ w_{12} - w_{13} & w_{22} - w_{23} \end{pmatrix}, w = \begin{pmatrix} w_{02} - w_{01} \\ w_{03} - w_{02} \end{pmatrix} \tag{2.19} \end{equation} }$

したがって、解はMの逆行列を解いて、

${ \displaystyle \begin{equation} \begin{pmatrix} x_1 \ x_2 \end{pmatrix} = M^{-1}w \tag{2.20} \end{equation} }$

となる。以上から、w01,w11,w21,w02,w12,w22,w03,w13,w23を調整することにより、(x1,x2)平面を３つの領域に分割できる事がわかる。このように１次関数を用いて直線的に領域を分割する仕組みを線形多項分類器と呼ぶ。

2.2.2　ソフトマックス関数による確率への変換

2.1.1ではf(x1,x2)の値をシグモイド関数を用いて確率Pに変換していた。一方、ここでは次の３つの確率を割り当てることが目標となる。

P1(x1,x2): (x1,x2)が領域１に属する確率
P2(x1,x2): (x1,x2)が領域２に属する確率
P3(x1,x2): (x1,x2)が領域３に属する確率

これは例えば、手書きの文字が「あ」である確率、「い」である確率、「う」で確率に計算される状況を考えれば良い。これらの確率は次の３式を満たす必要がある。

${ \displaystyle \begin{equation} 0 \leq P_i(x_1,x_2) \leq 1 \ (i=1,2,3) \tag{2.21} \end{equation} }$

${ \displaystyle \begin{equation} P_1(x_1,x_2)+P_2(x_1,x_2)+P_3(x_1,x_2)=1 \tag{2.22} \end{equation} }$

${ \displaystyle \begin{equation} f_i(x_1,x_2) > f_j(x_1,x_2) \Rightarrow P_i(x_1,x_2) > P_j(x_1,x_2) \ (i,j=1,2,3) \tag{2.23} \end{equation} }$

そして、これらを満たす式がソフトマックス関数と呼ばれ、次式で表される。

${ \displaystyle \begin{equation} P_i(x_1,x_2)= \frac{e^{f_i(x_1,x_2)}}{e^{f_1(x_1,x_2)}+e^{f_2(x_1,x_2)}+e^{f_3(x_1,x_2)}} \ (i=1,2,3) \tag{2.24} \end{equation} }$

以上の話をより一般化して書くと、座標(x1,x2,...,xM)を持つM次元空間をK個の領域に分割する場合、まず全部でK個の１次関数を用意する。

${ \displaystyle \begin{equation} f_k(x_1,...,x_M)=w_{0k} + w_{1k}x_1+...+w_{Mk}x_M \ (k=1,...,K) \tag{2.25} \end{equation} }$

そして、点(x1,x2,...,xM)がk番目の領域である確率はソフトマックス関数を用いて、次式で表される。

${ \displaystyle \begin{equation} P_k(x_1,...,x_M)= \frac{e^{f_k(x_1,...x_M)}}{\sum_{K'=1}^{K}e^{f_{k'}(x_1,...,x_M)}} \tag{2.26} \end{equation} }$

2.3　多項分類器による手書き文字の分類

ここからは前節の多項分類器を使って、手書き文字の分類問題を解いていく。

2.3.1　MNISTデータセットの利用方法

MNISTというデータセットを用いる。このデータセットにはトレーニング用の55000個のデータとテスト用の10000個のデータ、検証用の5000個のデータからなる。TensorFlowにはMNISTのデータセットをダウンロードしてNumPyのarrayオブジェクトとして格納するモジュールが予め用意されている。

#モジュールのインポート
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data

#MNISTデータセットのダウンロード
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)

#10個のデータを取り出し、画像データとラベルの変数に格納
images, labels = mnist.train.next_batch(10)

ここまでで、MNISTのデータ10個を変数に格納できた。対応するラベルを次に表示してみよう。

#対応するラベルのデータを表示してみる
print labels[0]

[ 0.  0.  0.  0.  0.  0.  0.  1.  0.  0.]

これを見ると、先頭から7番目の要素が1になっている。これはこの画像が「７」であることを表す。このように機械学習のデータセットではデータを幾つかのグループに分類する際に、k番目の要素のみが1になっているベクトルでk番目のグループであることを示す場合がある。これを1-of-Kベクトルを用いたラベル付けと呼ぶ。

#取り出した10個のデータの画像を表示してみる
fig = plt.figure(figsize=(8,4))
for c, (image, label) in enumerate(zip(images, labels)):
    subplot = fig.add_subplot(2,5,c+1)
    subplot.set_xticks([])
    subplot.set_yticks([])
    subplot.set_title('%d' % np.argmax(label))
    subplot.imshow(image.reshape((28,28)), vmin=0, vmax=1,
                   cmap=plt.cm.gray_r, interpolation="nearest")

表示される画像は以下のようになる。

f:id:tosh419:20161011210000p:plain

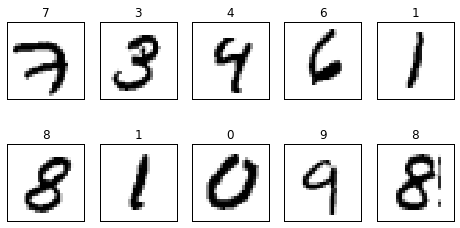
2.3.2　画像データの分類アルゴリズム

上の画像データに対して、多項分類器による分類手法を適用していく。先程の画像は28×28ピクセルの画像だ。これは28×28=784個の数値、784次元空間の１つの点(x1,x2,...,x784)に対応することになる。この時、同じ数字に対応する画像は784次元空間上で互いに近い場所に集まっていると考えられる。そのため、個のデータを784次元空間上でどの領域に属するかによって、どの数字の画像かを予測することが可能となる。

まず784次元空間のデータを0〜9の10種類の領域に分割するので、M=784、K=10としておく。そして、トレーニングセットのデータが全部でN個あるものとして、n番目のデータをxn=(x1n,x2n,...,xMn)と表し、さらにこれらを並べた行列Xを定義する。

${ \displaystyle \begin{equation} X=\begin{pmatrix} x_{11} & x_{21} & ... & x_{M1} \\ x_{12} & x_{22} & ... & x_{M2} \\ . & . & . & . \\ . & . & . & . \\ . & . & . & . \\ x_{1N} & x_{2N} & ... & x_{MN} \end{pmatrix} \tag{2.27} \end{equation} }$

次に、(2.25)式の１次関数の係数を並べた行列W、および定数項を並べたベクトルwを次式で定義する。

${ \displaystyle \begin{equation} X=\begin{pmatrix} w_{11} & _{12} & ... & w_{1K} \\ w_{21} & w_{22} & ... & w_{2K} \\ . & . & . & . \\ . & . & . & . \\ . & . & . & . \\ w_{M1} & w_{M2} & ... & w_{MK} \end{pmatrix}, \begin{pmatrix}w_{01},w_{02},...,w_{0K} \end{pmatrix} \tag{2.28} \end{equation} }$

これらから(2.25)は

${ \displaystyle \begin{equation} F=XW \oplus w \tag{2.29} \end{equation} }$

とまとめて計算される。

続いて、(2.26)のソフトマトリックス関数を使って、確率の値に変換する。今回は、n番目のデータxnに対して、これがk=1,...,Kのそれぞれに属する確率Pk(xn)を計算する。

${ \displaystyle \begin{equation} P_k(x_n) = \frac{e^{f_k(x_n)}}{\sum_{k'=1}^{K}e^{f_{k'}(x_n)}} \tag{2.32} \end{equation} }$

tensorflowではこれをきちんと行列演算で行ってくれる関数tf.nn.softmaxが用意されていて、

${ \displaystyle \begin{equation} P=tf.nn.softmax(F) \tag{2.33} \end{equation} }$

で求められる。これで、与えられた画像データに対してそれが0から9のいずれかである確率を計算するための数式が用意できた。新しいデータx=(x1,x2,...,xM)に対する確率を計算する際は(2.27)のXを次の1xM行列として用意する。

${ \displaystyle \begin{equation} X=(x_1 x_2 ... x_M) \tag{2.35} \end{equation} }$

これを用いて、(2.29)と(2.33)の計算を行うと、Pは次の1xM行列になることが分かる。

${ \displaystyle \begin{equation} X=(P_1(x) P_2(x) ... P_K(x)) \tag{2.36} \end{equation} }$

tensorflowのコードで言うと、xはPlaceholderに相当する。次に、誤差関数を用意する。これには最尤推定法を用いる。たとえば、n番目のデータxnの正解がkだった場合、正解を予測する確率はPk(xn)ということになる。ここで、一般にtn=(t1n,t2n,...,tKn)と表すと、n番目のデータに対して、正解を予測する確率Pnは

${ \displaystyle \begin{equation} P_n = \prod_{k'=1}^{K} {P_{k'}(x_n)}^{t_{k'n}} \tag{2.38} \end{equation} }$

また、すべてのデータに対して正解する確率Pは個々のデータに正解する確率の掛け算で決まる、

${ \displaystyle \begin{equation} P = \prod_{n=1}^{N} P_n = \prod_{n=1}^{N} \prod_{k'=1}^{K} {P_{k'}(x_n)}^{t_{k'n}} \tag{2.39} \end{equation} }$

このあとは(2.7)と同じく、誤差関数Eを最小化するために、確率Pを最大化する。

${ \displaystyle \begin{equation} E = -\log P \tag{2.40} \end{equation} }$

これは対数関数の公式より、

${ \displaystyle \begin{equation} E=-\sum_{n=1}^{N} \sum_{k'=1}^{K} t_{k'n}\log P_{k'}(x_n) \tag{2.41} \end{equation} }$

と書き直せる。この誤差関数Eを行列形式で表すためにはブロードキャストルールとTensorFlowのtf.reduce_sum関数を利用する。結局誤差関数Eは

${ \displaystyle \begin{equation} E = -tf.reduce_sum(T*\log P) \tag{2.43} \end{equation} }$

と表せる。いよいよTensorFlowのコードに入っていく。

#MNISTのデータセットを取得するモジュールをインポート
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data

np.random.seed(20160604)

#MNISTのデータセットをダウンロード
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)

#トレーニングセットのデータに対して、領域に属する確率Pk(xn)を計算する数式を定義
#xの要素数784は画像のピクセル数に一致して28x28=784
x = tf.placeholder(tf.float32, [None, 784])
w = tf.Variable(tf.zeros([784, 10]))
w0 = tf.Variable(tf.zeros([10]))
f = tf.matmul(x, w) + w0
p = tf.nn.softmax(f)

#誤差関数Eの定義
t = tf.placeholder(tf.float32, [None, 10])
loss = -tf.reduce_sum(t * tf.log(p))
train_step = tf.train.AdamOptimizer().minimize(loss)

#正解率を表す関係式の定義
#tf.argmaxは複数の要素が並んだリストから最大値を持つ要素のインデックスを返す関数。
#確率Pkのなかでも最大の確率となる文字がラベルで指定された正解の文字と一致するかを確認している
correct_prediction = tf.equal(tf.argmax(p, 1), tf.argmax(t, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

#セッションを準備する
sess = tf.InteractiveSession()
sess.run(tf.initialize_all_variables())

#勾配降下法によるパラメータの最適化を実施する
i = 0
for _ in range(2000):
    i += 1
#トレーニングセットから100個のデータを取り出す
    batch_xs, batch_ts = mnist.train.next_batch(100)
#勾配降下法によってパラメータの修正を行う
    sess.run(train_step, feed_dict={x: batch_xs, t: batch_ts})
    if i % 100 == 0:
        loss_val, acc_val = sess.run([loss, accuracy],
            feed_dict={x:mnist.test.images, t: mnist.test.labels})
        print ('Step: %d, Loss: %f, Accuracy: %f'
               % (i, loss_val, acc_val))

#得られた結果を実際の画像で確認する
images, labels = mnist.test.images, mnist.test.labels
p_val = sess.run(p, feed_dict={x:images, t: labels}) 

fig = plt.figure(figsize=(8,15))
for i in range(10):
    c = 1
    for (image, label, pred) in zip(images, labels, p_val):
        prediction, actual = np.argmax(pred), np.argmax(label)
        if prediction != i:
            continue
        if (c < 4 and i == actual) or (c >= 4 and i != actual):
            subplot = fig.add_subplot(10,6,i*6+c)
            subplot.set_xticks([])
            subplot.set_yticks([])
            subplot.set_title('%d / %d' % (prediction, actual))
            subplot.imshow(image.reshape((28,28)), vmin=0, vmax=1,
                           cmap=plt.cm.gray_r, interpolation="nearest")
            c += 1
            if c > 6:
                break

これを実行すると以下の結果が得られる。

f:id:tosh419:20161015213732p:plain

画像の添字としてついている数字は左が予測と右が正解になる。0/0となっているのは正解で、0/4となっていたら不正解になる。

2.3.4　ミニバッチと確率的勾配降下法

上のコードでも用いているミニバッチによるパラメータ修正について。そもそも確率降下法とはパラメータ(w0,w1,...)の関数として、誤差関数E(w0,w1,...)が与えられた際に、Eの値が減少する方向にパラメータを修正していくという考えだった。この時、Eの値が減少する方向は次の勾配ベクトルで決まるのだった。

${ \displaystyle \begin{equation} \nabla E = \begin{pmatrix} \frac{\partial E}{\partial w_0} \\ \frac{\partial E}{\partial w_1} \\ . \\ . \\ . \end{pmatrix} \tag{2.44} \end{equation} }$

ここで、誤差関数(2.41)式を見ると、トレーニングセットのそれぞれのデータについて和を取る形になっている。つまり、次のようにn番目のデータに対する誤差Enの和の形に分解することが可能になる。

${ \displaystyle \begin{equation} E=\sum_{n=1}^{N} E_n \tag{2.45} \end{equation} }$

ここで、Enは

${ \displaystyle \begin{equation} E_n=-\sum_{k'=1}^{K} t_{k'n} \log P_{k'}(x_n) \tag{2.46} \end{equation} }$

である。この時、Placeholder xにトレーニングセットの一部のデータだけを格納したとすると、対応する誤差関数lossはどのようになるだろうか。これは(2.45)式においてxに格納したデータの部分だけEnを足すということになる。この状態でトレーニングをするということは誤差関数Eにおいて、一部のデータからの寄与だけを考えて、データによる誤差を小さくするようにパラメータを修正することになる。本来のE全体の値を小さくするわけではないので、誤差関数の谷を一直線に下るのではなく、少しだけ横にずれた方向に下ることになる。ただし、次の修正処理においては、また違うデータからの寄与を考慮する。これを何度も繰り返すと、誤差関数の谷をジグザグに降りながら、最終的には本来の最小値に近づいていくと考えられる。これがミニバッチの考え方だ。一直線に最小値に向かわず、ランダムに最小値に向かうので、確率的勾配降下法とも呼ばれる。

確率的勾配降下法を用いることの利点として、

ミニバッチでは１回あたりのデータ量を減らして、最適化の処理を何度も繰り返すので、１回あたりの計算量を減らせる
最小値と極小値を持つような誤差関数の場合、極小値を避けて、真の最小値に達することができる

というものがある。これ以降、MNISTのデータセットを用いるコードでは、ミニバッチの最適化処理を適用する。

2016-10-10

TensorFlowで学ぶディープラーニング入門備忘録【第１章】

TensorFlowで学ぶディープラーニング入門 ~畳み込みニューラルネットワーク徹底解説~

作者: 中井悦司
出版社/メーカー: マイナビ出版
発売日: 2016/09/27
メディア: 単行本（ソフトカバー）
この商品を含むブログを見る

上記TensorFlowで学ぶディープラーニング入門という本を買ったので、その備忘録。

第１章　TensorFlow入門

1.1　ディープラーニングとTensorFlow

1.1.1　機械学習の考え方

月々の平均気温を予測する場合、月々の平均気温の測定値（データ）になめらかな曲線を描く。与えられたデータの数値をそのまま受け取るのではなく、その背後にある仕組みを考える→データのモデル化

今回の場合、平均気温の測定値を次の四次関数で表すとする。

${ \displaystyle \begin{equation} y=w_0+w_1x+w_2x^{2}+w_3x^{3}+w_4x^{4} \tag{1.1} \end{equation} }$

予想したモデルの正確性の評価にはモデルから予測される値と実際のデータの誤差で判断する。 すなわち、モデル式にx=1,2,...12を代入して得られる予想平均気温をy1,y2,...y12とすれば、

${ \displaystyle \begin{equation} E = \frac{1}{2} \sum_{n=0}^{12} (y_n - t_n)^{2} \tag{1.2} \end{equation} }$

として二乗誤差は表され、これが、月々の予測値と実データの差の二乗を計算した値となっている。(1.2)式の係数w0〜w4を調整することで、それらしい曲線を得られる。(1.2)は係数w0〜w4の関数とみなせるので、誤差関数と呼ぶ。

ここまでを整理すると、

与えられたデータをもとにして、未知のデータを予測する数式を考える
数式に含まれるパラメータの良し悪しを判断する誤差関数を用意する
誤差関数を最小にするようにパラメータの値を決定する

ということになる。これを本書では機械学習モデルの３ステップと呼ぶ。

1.1.2ニューラルネットワークの必要性

あるウイルスに感染しているかしていないかというデータの分類問題を考える。検査結果は２種類の数値(x1,x2)で与えられるものとし、この２つの数値をもとにしてウイルスに感染している確率を求める。本書中の散布図データを見ると、検査結果は大きく直線で分類できそうで、

${ \displaystyle \begin{equation} f(x_1,x_2) = w_0 + x_1 x_1 + w_2 x_2 = 0 \tag{1.3} \end{equation} }$

という数式で表現できそうである。平面上の直線というと、y=ax+bという形式が有名だが、ここではx1とx2を対称に扱うためにこのような形式を用いている。また、この形式の利点として、f(x1,x2)=0が境界となる他に境界から離れるほどに、f(x1,x2)の値が±∞にむかって増加していくという性質がある。そこで、0から1に向かってなめらかに値が変化するシグモイド関数σ(x)を用意して、これにf(x1,x2)の値を代入すると、検査結果(x1,x2)から感染確率P(x1,x2)を求める関数を作ることができる。ここでシグモイド関数を使う利点としては入力する値がどんなに大きくても小さくても、0〜1の間に出力が収まることである。

${ \displaystyle \begin{equation} P(x_1,x_2)=\sigma(f(x_1,x_2)) \tag{1.4} \end{equation} }$

ところで、今回与えられたデータは直線で分類できる前提条件に従っていたが、これが、折れ曲がった直線あるいは曲線を用いて分類する必要があるデータであったらどうだろう。単純にはより複雑な数式に置き換えれば良さそうだが、現実には難しい。今回は数値が２種類であったが、これが全部で２０種類だったらどうだろう。２０次元のグラフが必要になってしまう。

そんな中、より柔軟性が高く様々なデータに対応できる数式を考え出す努力が行われてきたが、それの一つがニューラルネットワークになる。

まず最もシンプルなニューラルネットワークを示す。

左から(x1,x2)という値のペアを入力すると、内部でf(x1,x2)の値が計算されて、それをシグモイド関数σ(x)で0〜1の値に変換したものが、変数zとして出力される。これはニューラルネットワークを構成する最小のユニットでノードと呼ばれる。

このノードを多層に重ねることで、より複雑なニューラルネットワークが得られる。２層のノードからなるニューラルネットワークを以下に示す。

このニューラルネットワークにはw10,w11,w12,w20,w21,w22,w0,w1,w2の９つのパラメータが含まれており、これらの値を調整することで、単なる直線でない、より複雑な境界線が表現できる。原理的にはノードの数を増やしていけば、どんな複雑な境界線でも書くことが可能だ。しかしながら、パラメータの数が膨大になってそれではパラメータの最適化が終わらない。機械学習におけるニューラルネットワークの挑戦は実際に計算が可能で、かつデータの特性にあった、ニューラルネットワークを構成するという点にある。この挑戦を続ける中で、出てきた特別な形のニューラルネットワークがディープラーニングだ。

1.1.3　ディープラーニングの特徴

ディープラーニングは基本的には多層ニューラルネットワークを用いた機械学習に過ぎないが、単純に層を増やして複雑化するのではなく、解くべき問題に応じて、それぞれのノードに特別な役割を与えたり、ノード間の接続を工夫したりということを行う。

例えば、先程のニューラルネットワークではそれぞれのノードは単純な１次関数とシグモイド関数の組み合わせになっていたが、CNN(畳み込みニューラルネットワーク)では１層目のノードには１次関数ではなく、畳込みフィルターなる関数を用いている。また、その後ろのプーリング層では画像の解像度を落とす処理を行う。これは画像の詳細をあえて消し去り、描かれている物体の本質的な特徴のみを抽出しようとする発想による。このような前処理を行ったデータを更に後段のノードが解析し、なんの画像なのかを判断する。あるいはRNN(リカレントニューラルネットワーク)という例もある。一般には時系列データを取り扱うものだが、一例として、単語が並んだ文章などの自然言語処理に応用される。

これはある文章が自然な文章か不自然な文章かを見分ける。This is a penという文章に対して、Thisのあとにisが来る確率、isのあとにaが来る確率などを順番に見ていき、全てが高確率になっていれば自然な文章だと判断する。この時、はじめにThisを入力して、次にisを入力する際、その前にThisを入力した際の中間層の出力値もあわせて入力する。先程の中間層にはその前にThisを入力した際の中間層の出力値も合わせて入力する。中間層には最初の単語がThisであったという情報が、isであるという情報だけよりもさらに自然な予測ができる。このように、上図の仕組みでは、過去の入力値の情報が中間層に蓄積されていくことで、より長い単語列に基づいた判断ができる、つまり過去の中間層の値を次の入力に再利用するニューラルネットワークがRNNだ。

1.1.4　TensorFlowによるパラメータの最適化

これからTensorFlowが何をしているか、を(1.2)の誤差関数Eを例に評価する。 (1.2)式に含まれるynはn月の気温を(1.1)式で予測した結果を表す。つまり、

${ \displaystyle \begin{equation} y_n = w_0 + w_1n +w_2n^{2}+w_3n^{3}+w_3n^{4} = \sum_{m=0}^{4} w_mn^{m} \tag{1.7} \end{equation} }$

(1.7)式を(1.2)式に代入すると、次式が得られる。

${ \displaystyle \begin{equation} E(w_0,w_1,w_2,w_3,w_4) = \frac{1}{2} \sum_{n=1}^{12} \ (\sum_{m=0}^{4} w_mn^{m} - t_n)^{2} \tag{1.8} \end{equation} }$

これで誤差関数がわかったので、(1.8)を最小にするw0〜w4を決定する。つまり、(1.8)をw0〜w4のそれぞれで偏微分した値を0とした、次の連立方程式を解くことになる。

${ \displaystyle \begin{equation} \frac{\partial E}{\partial w_m}(w_0,w_1,w_2,w_3,w_4)=0 \ (m=0,...,4) \tag{1.9} \end{equation} }$

ここで、話を簡単にするために、次の２変数関数を用いて、なぜ上式の条件で、Eが最小になるかを説明する。

${ \displaystyle \begin{equation} h(x_1,x_2) = \frac{1}{4}(x_1^{2}+x_2^{2}) \tag{1.11} \end{equation} }$

これの偏微分は、

${ \displaystyle \begin{equation} \frac{\partial h}{\partial x_1}(x_1,x_2)=\frac{1}{2}x_1,\ \frac{\partial h}{\partial x_2}(x_1,x_2)=\frac{1}{2}x_2 \tag{1.12} \end{equation} }$

またこれらを並べたベクトルを次の記号で表して、関数h(x1,x2)の勾配ベクトルと呼ぶ。

${ \displaystyle \begin{equation} \nabla h(x_1,x_2)=\begin{pmatrix} \frac{1}{2}x_1\ \frac{1}{2}x_2 \end{pmatrix} \tag{1.13} \end{equation} }$

勾配ベクトルはすり鉢の壁を登っていく方向に一致し、勾配ベクトルの大きさは壁を登る傾きに一致する。壁の傾きが大きいほど、勾配ベクトルも長くなる。すり鉢の壁を降りていくに従い、傾きは小さくなるので、勾配ベクトルの大きさもだんだん小さくなる。この例の場合、最終的に原点(0,0)に達したところで、h(x1,x2)は最小となるので、勾配ベクトルの大きさも0になる。つまり、h(x1,x2)を最小にする(x1,x2)は∇h(x1,x2)=0という条件で決まることになる。現在の位置をx=(x1,x2)T（注：Tは転置の意味）とすれば、新しい位置は

${ \displaystyle \begin{equation} X^{new} = x - \nabla h \tag{1.14} \end{equation} }$

として表され、これを何度も繰り返すと、どこから出発したとしても、次第に原点に近づいていく。このように勾配ベクトルを計算して、反対方向にパラメータを修正するアルゴリズムを勾配降下法と呼ぶ。気をつけならないのが、パラメータを修正する分量だ。例として以下の例に適用してみよう。

${ \displaystyle \begin{equation} h_1(x_1,x_2)=\frac{3}{4}(x_1^{2}+x_2^{2}) \tag{1.15} \end{equation} }$

${ \displaystyle \begin{equation} h_2(x_1,x_2)=\frac{5}{4}(x_1^{2}+x_2^{2}) \tag{1.16} \end{equation} }$

それぞれの勾配ベクトルは

${ \displaystyle \begin{equation} \nabla h_1 = \frac{3}{2} \begin{pmatrix} x_1\ x_2 \end{pmatrix} \tag{1.17} \end{equation} }$

${ \displaystyle \begin{equation} \nabla h_1 = \frac{5}{2} \begin{pmatrix} x_1\ x_2 \end{pmatrix} \tag{1.18} \end{equation} }$

例えば、式(1.17)を適用しながら移動すると始点を(1,-1)と仮定し、(1,-1)-3/2(1,-1)=(-1/2,1/2)→(-1/2,1/2)-3/2(-1/2,1/2)=(1/4,-1/4)→(1/4,-1/4)-3/2(1/4,-1/4)=(-1/8,1/8)などと、0に漸近していくことが分かる。一方、式(1.18)を適用していくと、始点を(1,-1)として、(1,-1)-5/2(1,-1)=(-3/2,3/2)→(-3/2,3/2)-5/2(-3/2,3/2)=(3,-3)などと、原点から離れていってしまうことが分かる。このように、うまくパラメータが原点にうまく近づくことを収束する、逆に最小値から遠ざかってしまうことを発散するという。そして、この移動量は学習率εとして表現され、式(1.14)は

${ \displaystyle \begin{equation} X^{new} = x - \epsilon \nabla h \tag{1.19} \end{equation} }$

に変形できる。この学習率は一回の更新でパラメータをどの程度修正するかのパラメータになり、小さすぎると最小値に達するまでの時間がかかる一方、大きすぎると、パラメータが発散して最適化ができない。

なお、今回は２変数関数で考えたが、当然、変数が増えても同様の考え方が適用可能だ。式(1.8)の二乗誤差Eを最小にするパラメータw0〜w4を決定する場合であれば、これを並べたベクトルw=(w0,w1,w2,w3)Tとして、

${ \displaystyle \begin{equation} w^{new} = w - \epsilon \nabla E(w) \tag{1.20} \end{equation} }$

${ \displaystyle \begin{equation} \nabla E(w) =\begin{pmatrix} \frac{\partial E}{\partial w_0} \ . \ . \ . \ \frac{\partial E}{\partial w_4} \end{pmatrix} \tag{1.21} \end{equation} }$

を計算すれば良い。この時(1.20)でパラメータを更新するたびに、その点における勾配ベクトルの値を(1.21)で計算し直す事が必要だ。

1.2　環境準備

TensorFlowの環境準備をCentOS7のDockerコンテナでJupyterを起動して、外部のwebブラウザからアクセスして使用するまでの環境準備が説明されている。私の場合、MacOS(El Capitan)なので、巻末付録を参考に環境構築した。

Macの場合も、DockerコンテナでJupyterを起動して、ローカルのwebブラウザからアクセスして使用する。 ①まず以下の、Docker HPよりDocker for Macをダウンロードする。

Docker | Docker

②インストールは特に難しくないはずなので、設定へ

上部メニューバーのクジラのアイコンからPreferences→MemoryとCPUの使用率をそれぞれ4GB、4個以上にして、再起動する。

③Macのターミナルより、以下を打つ。

$ mkdir $HOME/data
$ docker run -itd --name jupyter -p 8888:8888 -p 6006:6006 \
       -v $HOME/data:/root/notebook -e PASSWORD=passw0rd \
       enakai00/jupyter_tensorflow:0.9.0-cp27

実際にうってみた感じは以下のよう。

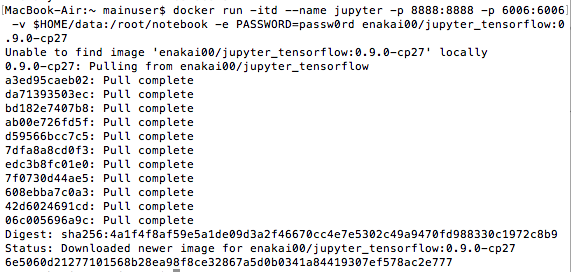
-e PASSWORDオプションはブラウザからJupyterにアクセスする際の認証パスワードである。この手順でコンテナを起動した場合、Jupyterで作成したノートブックのファイルは、ユーザのホームディレクトリーの下のdataディレクトリに保存される。ブラウザからJupyterに接続する場合、http://localhost:8888にアクセスし、TensorBoardの画面のアクセスにはhttp://localhost:6006からアクセスする。

1.2.2　Jupyterの使いかた

Jupyterではノートブックと呼ばれるファイルを開いて、その中でPythonのコマンドやプログラムを対話的に実行していく。①つのノートブックは複数のセルに分かれており、１つのセルには実行するべきコマンドとその実行結果がセットで記録される。早速、http://localhost:8888にアクセスし、ノートブックを作ってみる。

このあたりは本を買っていればサッと飛ばせる話なので省略する。

1.3　TensorFlowクイックツアー

まずは月々の平均気温を予測する問題をTensorFlowを用いて解いていく。

1.3.1　多次元配列によるモデルの実現

TensorFlowでは計算に用いるデータはすべて多次元配列として表現する。例えば、n月の予測気温ynは式(1.7)を行列を用いると、

${ \displaystyle \begin{equation} y_n = (n^{0},n^{1},n^{2},n^{3},n^{4}) \begin{pmatrix} w_0 \ w_1 \ w_2 \ w_3 \ w_4 \end{pmatrix} \tag{1.22} \end{equation} }$

として表される。さらに12ヶ月分のデータは

${ \displaystyle \begin{equation} y=Xw \tag{1.23} \end{equation} }$

${ \displaystyle \begin{equation} y_n = \begin{pmatrix} y_1 \\ y_2 \\ . \\ . \\ . \\ y_{12} \end{pmatrix},X=\begin{pmatrix} 1^{0} &1^{1} &1^{2} &1^{3} &1^{4} \\ 2^{0} &2^{1} &2^{2} &2^{3} &2^{4} \\ . \\ . \\ . \\ 2^{0} &12^{1} &12^{2} &12^{3} &12^{4} \end{pmatrix},w=\begin{pmatrix} w_0 \\ w_1 \\ w_2 \\ w_3 \\ w_4 \end{pmatrix} \tag{1.24} \end{equation} }$

として表される。Xはトレーニングセットとして与えられたデータから構成される。TensorFlowではこのようなトレーニングセットを保存する変数をPlaceholderと呼ぶ。次に、wはこれから最適化を実施するパラメータでありVariableと呼ぶ。そして、yはPlaceholderとVariableから計算される値になる。パラメータの最適化を実施するには二乗誤差を求める必要があるが、これは予測値yとトレーニングセットのデータtから計算されるものである。tは次のようにn月の平均気温を縦に並べたベクトルである。

${ \displaystyle \begin{equation} t=\begin{pmatrix} t_1 \ t_2 \ . \ . \ . \ t_{12} \end{pmatrix} \tag{1.25} \end{equation} }$

ただし、このままでは(1.6)を行列形式にはできないので新しい演算を定義する。一般のベクトルv=(v1,v2,...,v_N)Tに対して、次の演算を定義する。

${ \displaystyle \begin{equation} square(v)= \begin{pmatrix} v_1^{2} \ v_2^{2} \ . \ . \ . \ v_N^{2} \end{pmatrix} \tag{1.26} \end{equation} }$

${ \displaystyle \begin{equation} reduce\_sum(v)= \sum_{i=1}^{N} v_i \tag{1.27} \end{equation} }$

squareは、ベクトルの各成分を二乗するもので、reduce_sumはベクトルの各成分の和を計算する。これらの演算を利用すると、(1.6)は

${ \displaystyle \begin{equation} E = \frac{1}{2}reduce\_sum(square(y-t)) \tag{1.28} \end{equation} }$

と表される。これで、誤差関数を行列方式、多次元配列方式で表現できた。

1.3.2　TensorFlowのコードによる表現

ここからは、実際にJupyter上でTensorFlowのコードを実行する。

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

これはライブラリのインポートなので、問題ないと思う。

x = tf.placeholder(tf.float32, [None, 5])
w = tf.Variable(tf.zeros([5, 1]))
y = tf.matmul(x, w)

トレーニングセットのデータを保持するXを用意するが、[None, 5]と引数を指定している。これは任意の行数と５列の行列で初期化することを意味する。

次に、誤差関数を表現する。

t = tf.placeholder(tf.float32, [None, 1])
loss = tf.reduce_sum(tf.square(y-t))

tは12×1行列に相当するが、データ数の部分を任意に取れるようにするため、[None, 1]というサイズ指定を行っている。次に、トレーニングアルゴリズムを選択する。

train_step = tf.train.AdamOptimizer().minimize(loss)

tf.train.AdamOptimizer()は与えられたトレーニングセットのデータから誤差関数を計算して、その勾配ベクトルの反対方向にパラメータを修正するものだ。学習率は自動的に調整する機能を持っている。

sess = tf.Session()
sess.run(tf.initialize_all_variables())

まずは実行環境となるセッションを用意する。次に、トレーニングアルゴリズムの実行をセッション内で行う。

train_t = np.array([5.2, 5.7, 8.6, 14.9, 18.2, 20.4, 25.5, 26.4, 22.8, 17.5, 11.1, 6.6])
train_t = train_t.reshape([12,1])
train_x = np.zeros([12, 5])
for row, month in enumerate(range(1, 13)):
      for col, n in enumerate(range(0, 5)):
            train_x[row][col] = month**n

ここでは、tとXをarrayオブジェクトとして用意した。

i = 0
for _ in range(100000):
     i += 1
     sess.run(train_step, feed_dict={x:train_x, train_t})
     if i % 10000 == 0:
     loss_val = sess.run(loss, feed_dict={x:train_x, train_t})
     print ('Step: %d, Loss: %f' % (i, loss_val))

ここでは、勾配降下法によるパラメータの最適化を実施している。

for _ in range(100000):
     i += 1
     sess.run(train_step, feed_dict={x:train_x, t:train_t})
     if i % 10000 == 0:
        loss_val = sess.run(loss, feed_dict={x:train_x, t:train_t})
        print ('Step: %d, Loss: %f' % (i, loss_val))

更に100000回だけトレーニングを実施している。すると、Lossがあるところから増加に転じる。そこでトレーニングを打ち切って、その時点でのパラメータの値を確認する。

w_val = sess.run(w)
print w_val

続いて、この結果を用いて、予測気温を表す関数を定義する。

def predict(x):
       result = 0.0
       for n in range(0, 5):
             result += w_val[n][0] * x**n
       return result

fig = plt.figure()
subplot = fig.add_subplot(1,1,1)
subplot.set_xlim(1,12)
subplot.scatter(range(1,13), train_t)
linex = np.linspace(1,12,100)
liney = predict(linex)
subplot.plot(linex, liney)

上のコードには関数をプロットするものも入っており、これを実行すると、以下のグラフが得られる。

f:id:tosh419:20161010152546p:plain

ここまでで、第１章は終わりになる。

2016-07-30

正規表現技術入門　備忘録（第1章）

業務アプリでオートコンプリートとかその辺りを触っている関係で正規表現技術入門という本を読んでいる。正規表現は全くの未経験なので、まずは深いところはスキップして、基本的なところを抑えていこうと思う。なお、現時点で正規表現の専門的な知識は必要としていないので、第1章だけの備忘録になる。

正規表現技術入門 ――最新エンジン実装と理論的背景 (WEB+DB PRESS plus)

作者: 新屋良磨,鈴木勇介,高田謙
出版社/メーカー: 技術評論社
発売日: 2015/04/14
メディア: 単行本（ソフトカバー）
この商品を含むブログ (1件) を見る

正規表現とは何か

正規表現は英語で「regular expression」と言い、一種の表現（ものの書き方）である。例えば、

0|1|2|3|4|5|6|7|8|9

というのも一種の正規表現で、0から9までの数字という意味を表している。同様に、

1(0|1|2|3|4|5|6|7|8|9)

と書けば、10から19までの2桁の数字を意味する。このように丸括弧は正規表現を部品ごとに区切るために使われる。

もう少し複雑な例を見てみる。

03-[0-9][0-9][0-9][0-9]-[0-9][0-9][0-9][0-9]

という正規表現は03から始まる電話番号を表している。さらに、数学でx+x+x+xを4xと記述できるように、正規表現[0-9][0-9][0-9][0-9]は[0-9]{4}と短く書くことができる。{4}が4回繰り返すことを示していて、これを量指定子(quantifier)などとよんだりする。よって、上の例は、

03-[0-9]{4}-[0-9]{4}

さらには、

03(-[0-9]{4}){2}

[0-9]は\dとも書けるので最終的には

03(-\d{4}){2}

とかける。

正規表現において、特別な意味を持ったメタ文字と意味を持たないリテラルが存在する。上の例で言うと、[]-\dなどがメタ文字、0や9がリテラルだ。

リテラル
メタ文字
- 構成要素
- 演算子

さて、このような正規表現は実際にはどのように使われているのだろうか。身近なところではHTML5でメールアドレスを入力するフォームに

^[a-zA-Z0-9.!#$%&'*+/=?^_`{|}~-]+@[a-zA-Z0-9](?:[a-zA-Z0-9-]{0,61}[a-zA-Z0-9])?(?:\.[a-zA-Z0-9](?:[a-zA-Z0-9-]{0,61}[a-zA-Z0-9])?)*$

という正規表現が使われている。

正規表現の演算

正規表現の基本演算は

連接
選択
繰り返し

である。上のHTML5の正規表現のように[a-zA-Z0-9]と[a-zA-Z0-9-]{0,61}などとつなげて構成する。このつなげる演算を連接と呼ぶ。連接には特に演算子として特別な記号はない。hatenaという文字はhとaとtと、、を連接し成り立っているが、当たり前なため記号はないということだ。正規表現A|BはAもしくはBという意味を表す。この|で並べる演算を選択もしくは和と呼ぶ。次に繰り返しだが、正規表現\dは任意の長さの数字列を表現している。は0回以上、いくらでも繰り返されているパターンを表現する。

演算子の結合順位

四則演算で、掛け算の優先順位が高いように演算子にも順位があり、それは
繰り返し　＞　連接　＞　選択
というものだ。

正規表現のシンタックスシュガー

本来、正規表現には上記の3演算だけで事足りるはずだが、3演算だけで書くと複雑になってしまう場合がある。その場合に、簡単に書くための構文が追加されている。それがシンタックスシュガーだ。

プラス演算

+は1回以上の任意回の繰り返しを意味する。ab+cという正規表現があった時、acは該当せず、abcやabbbcなどのように少なくとも1文字以上のbを含んだ文字列を表現する。ab*cという正規表現は0回の繰り返しも含まれ、acという文字列にもマッチする。

疑問符演算

?をパターンの後ろにつけることで、パターンの0回か1回の繰り返しを表す。0回か1回の繰り返しというのは現れるか現れないかとも言い換えられる。例えば、https?://hogehoge.jpはHTTPとHTTPSのどちらもマッチする。s?となっておりあってもなくても良いからだ。

範囲量指定子

演算子{n,m}はn回からm回までの繰り返しを実現する演算子である。例えば、x{1,5}はxの1から5回の繰り返しを表し、x|xx|xxx|xxxx|xxxxxという正規表現と同様の表現になる。x{3,3}のように最小と最大の数字を同じ数字に揃えれば、ピッタリ3回の繰り返しを表現する。この場合、x{3}ともかける。範囲量指定子には{1, 3}のようにスペースを入れたり、{3,1}などと最大最小を逆転した書き方をしてはならない。

ドット

ドットは任意の一文字を表す。たとえばr.*eはrで始まり、eで終わる全部の文字列がマッチする。

文字クラス

0から9までの数字は[0-9]、小文字のみのアルファベットは[a-z]、大文字のみのアルファベットは[A-Z]、大文字も小文字も含むアルファベットは[a-zA-Z]と表す。文字クラスにおける[]の内部では-は範囲指定の記号として特別扱いされる。[a-z]のようにハイフンの前後に表現したい文字範囲の先頭と末尾の文字を記述することで文字範囲を表現する。^は否定を意味する。[^0-9A-Za-z]と書けば、数字やアルファベット以外の文字にマッチする。

エスケープシーケンス

エスケープシーケンスは\を用いて表す。

\a　…　ベル文字
\f　…　改ページ
\t　…　タブ
\n　…　改行
\r　…　復帰
\v　…　垂直タブ
\d　…　数字
\D　…　数字以外
\w　…　文字列記号
\W　…　文字列記号以外
\s　…　スペース
\S　…　スペース以外

アンカー

位置を表すアンカーは以下の様なものがある。Sublimeの置換などでもこれは使えるので便利。

^　…　行頭
$　…　行末
\A　…　テキスト先頭
\b　…　文字列の間
\B　…　文字列の間以外
\z　…　テキスト終端

キャプチャと置換

「文字列がどのようにパターンにマッチするか」という情報を使って文字列を操作するキャプチャと置換を扱う。キャプチャの前に、正規表現マッチングについており細かい点を解説する。

文字列の部位

文字列には部位がある。接頭辞(prefix)、接尾辞(suffix)、部分文字列(substring)だ。文字列sについて文字列tがsの

接頭辞であるとは、tがsの先頭の文字列であること
接尾辞であるとは、tがsの末尾の文字列であること
部分文字列であるとは、sがtを含むこと

を意味する。

マッチングの種類

正規表現によるマッチングには大きく分けて、以下の４種類がある。

完全一致：正規表現が与えられた文字列の全体にマッチ
前方一致：正規表現が与えられた文字列の接頭辞にマッチ
後方一致：正規表現が与えられた文字列の接尾辞にマッチ
部分一致：正規表現が与えられた文字列の部分文字列にマッチ

例えば、PythonやJavaScriptの標準の正規表現では、前方一致にmatch()メソッド、部分一致にsearch()メソッドを提供している。

丸括弧を使って正規表現を部分的に括ることができるが、丸括弧でまとめられた正規表現の一部はサブパターンと呼ぶ。サブパターンにマッチした部分文字列をサブマッチと呼ぶ。

部分一致がデフォルトな状況でのマッチングの種類の明示

マッチングの種類	正規表現
部分一致	regex
完全一致	^regex$
前方一致	^regex
後方一致	regex$

完全一致がデフォルトな状況でのマッチングの種類の明示

マッチングの種類	正規表現
部分一致	regex
完全一致	.regex.
前方一致	regex.*
後方一致	.*regex

例えば、(\d+): (\w+) prime.という正規表現には(\d+)と(\w+)の２つのサブパターンが含まれている。この正規表現に対して、57: Grothendieck prime.という文字列はマッチする。このとき、(\d+)に対しては57が、(\w+)にはGrothendieckが部分文字列としてマッチしている。よって、57とGrothendieckはそれぞれ(\d+)と(\w+)に対応するサブマッチとなる。

キャプチャ

正規表現と文字列からサブマッチを抜き出すことをキャプチャという。正規表現のあるサブパターンに対するサブマッチを取得するためには明示的に、特定のサブパターンに対するサブマッチを指定する必要がある。これには、

順番で指定する方法
名前で指定する方法

がある。

順番で指定する方法

サブパターンには自然な順番というものが存在する。１から順に開き括弧が左側にあるほど小さい番号を付けるという順序付けだ。たとえば、日／月／年を表す正規表現(\d{2})/(\d{2})/(\d{4})には日の２桁が１番、月の２桁が２番、年の４桁に３番という順番がつけられている。

名前で指定する方法

順番で指定する方法は、単純な一方、正規表現の変更に弱い。そこで、名前付きキャプチャを使う。名前付きキャプチャでは、サブパターンに好きな名前をつけて、その名前経由でサブマッチを取得することができる。PerlやRubyでは(?)という構文でサブパターンに名前をつけることができる。Perlで書いてみると、

$day = '14/11/1988';
if ($day =~ /(?<d>\d{2})\/(?<m>\d{2}\/(?<y>\d{4})/) {
  print "$+{y} 年 $+{m} 月 $+{d} 日";
#=> 1988年 11 月 14 日

正規表現の拡張機能

先読み

先読みとは、「与えられた正規表現がマッチする文字列が直後に来る位置」と正規表現を使って位置を指定することができる機能である。マッチング対象文字列が「abracadabra」だったとして、「a(?=..a)」はどの部分文字列にマッチし得るのか。実は「a(?=..a)」という正規表現は２箇所の「a」にしかマッチしない。先読み部分の正規表現「(?=..a)」はあくまで３文字先にaが来るという位置にマッチするためだ。

再帰

再帰演算子(?R)は正規表現の全体にマッチする。つまり、

A(?R)|B
A(A(?R)|B)|B
A(A(A(A(A(...)|B)|B)|B)|B)|B
A*B

上記再帰表現を展開しているとAが０回以上続いて、Bで終わるというパターンを表現している事がわかる。

後方参照

後方参照とはキャプチャによって取得した部分文字列をその正規表現の中で参照する機能だ。 (.) \1 は任意の文字列をスペースを挟んで２回繰り返した文字列にマッチする正規表現だ。つまり\1の部分が(.)を参照しており、 (.) (.) と等価に置き換えられる。

以上で、大体の１章の内容になる。２章以降は

第２章　正規表現の歴史
第３章　プログラマのための一歩進んだ正規表現
第４章　DFA型エンジン
第５章　VM型エンジン
第６章　正規表現エンジンの三大技術動向
第７章　正規表現の落とし穴
第８章　正規表現を超えて

といった進み方をするが、今回は一般教養として正規表現を使えるようになるのが目的だったので、一旦閉める。検索エンジンやコンパイラやプログラミング言語を作りたい方などは第２章以降も役に立つだろう。

2016-07-30

FPGA入門　備忘録④　〜順序回路編〜

備忘録③の続きになる。

RSフリップフロップ

f:id:tosh419:20160724205656p:plain

上図はORゲートを用いた状態記憶回路である。ORゲートの出力Qが一方の入力に帰還しているため入力Sが一度1になると、出力Qはその後、入力Sの状態にかかわらず1を保持し続ける。

f:id:tosh419:20160724210239p:plain

上図は、最初の回路にリセット入力Rを追加したもので、これにより出力Qを0に戻すことが可能になる。以下にRSフリップフロップの真理値表を示す。入力SとRが共に0の時は共に0となる直前の出力Qが保持される。ただし、直前の入力が共に0の時は、いずれの値が保持されるかは分からない。 Rが0でSが1の時、Q=1、Rが1でSが0の時はQ=0となる。R=1、S=1の時、Q=1となるが、この状態からR=0、S=0となった場合に、Q=1の保持が確実でないのは各ゲートの遅延などでR=1、S=0となってからR=0、S=0となる可能性があるためだ。そのため、R=1、S=1は一般に使わない。

入力		出力
R	S	Q
0	0	前の状態
0	1	1
1	0	0
1	1	1(使用禁止)

f:id:tosh419:20160724212938p:plain

上に簡略化の流れを示す。まずひとつ目の図はORゲートをNORゲートに変更して、ふたつ目の図のように書ける。次に、ふたつ目の図のANDゲートはNOTゲートと組み合わせて、３つめの図のようにNORゲートに置き換え可能だ。ここで、各NORゲートの出力をそれぞれQ、Q_とすると、４つ目の図のようになる。

４つ目の図の真理値表を書くと、

入力		出力
R	S	Q	Q'\|Q_
0	0	前の状態	前の状態\|前の状態
0	1	1	1\|0
1	0	0	0\|1
1	1	1	0\|0

ここで、前述のようにRとSが共に1の時に使わないのであれば、Q=Q'として更に、５つ目の図のように簡略化できる。

入力			出力
R	S	Q	Q_
0	1	1	0
1	0	0	1
1	1	0(使用禁止)	0(使用禁止)

最後に、５つ目の図は６つ目のよく見る図のように簡略化できる。簡略化しNORゲートのみを使って表すことで、回路規模が小さくできる。XilinxのFPGAではプリミティブとして、後述のDフリップフロップと同期セット・リセット入力付きDフリップフロップなどが用意されている。ただ、これらのプリミティブを用いずに基本ゲート(Look Up Table)のみを用いて、フリップフロップを構成することができる。

RSフリップフロップのverilogによる記述を示す。

module RSFF_VERILOG(SW0, SW1, LED0, LED1);

  input SW0;
  input SW1;
  output LED0;
  output LED1;

  assign LED0 = ~(SW0 | LED1);
  assign LED1 = ~(SW1 | LED0);

endmodule

Dフリップフロップ

RSフリップフロップはSにセットした値、もしくはRでリセットした値を時間経過に関係なく保持することができる1bitのメモリだ。しかし、その値を保持するためにはS=0、R=0という状態を保持する必要がある。これではまだ使い勝手が悪い。つまり実際の回路ではある瞬間のみに値の書き込みを行い、それ以降はSおよびRの状態と無関係に値を保持する動作を求められる。そのような動作を実現するために書き込む値を入力する端子と書き込み制御を行う端子を分離したフリップフロップの一つがDフリップフロップだ。このDフリップフロップと後で説明するクロックイネーブル入力付きDフリップフロップ、及び基本ゲートがあればほとんどの完全同期式回路を記述できる。

以下にDフリップフロップの回路シンボルと真理値表を示す。 f:id:tosh419:20160724215602p:plain

入力
D	CLK	Q
0	↑	0
1	↑	1
0	-	直前の値
1	-	直前の値

DフリップフロップはDの入力状態をCLKから入力される信号の立ち上がりエッジで取り込み、Qに出力する。Qの出力は次のCLKの立ち上がりエッジが来るまで、変化しない。特に断りがなければ、立ち上がりエッジで取り込むポジティブエッジタイプを使う。立ち下がりで取り込むネガティブエッジタイプのシンボルを参考までに以下に示す。

f:id:tosh419:20160724220601p:plain

RSフリップフロップはRとSを用いて、書き込むデータを表すとともに書き込むか、保持するかの動作の制御も行っていた。これに対し、Dフリップフロップではデータを入力するDと書き込み制御を行うCLKという風にデータ入力と制御入力を分離している。このデータと制御の分離は非常に重要で、大きな回路規模の設計を行うときには、データパスの設計なのか、制御パスの設計なのかを常に意識する必要がある。

Dフリップフロップのverilog記述を以下に示す。

module DFF_VERILOG(SW0, SW1, LED0);

  input SW0;
  input SW1;
  output LED0;

  reg LED0;

  always @(posedge SW1) begin
    LED0 <= SW0;
  end

endmodule

always文のところで、DFFの制御を書いている。SW1の立ち上がりエッジで、SW0の値が取り込まれ、LED0に出力される。

セットアップ時間とホールド時間

DフリップフロップはCLKに入力される信号の立ち上がりエッジでデータを取り込む。したがって、データ入力はCLKの立ち上がりエッジ以前に確定している必要がある。このCLKの立ち上がりエッジからデータが確定していなければならない時間がセットアップ時間tsである。また、内部のRS-FFが安定し、入力データがDフリップフロップに取り込まれるまでには時間を要する。したがって、入力データはCLKの立ち上がりエッジから特定の時間以上保持する必要があり、この時間がホールド時間thである。よって、ts+thの期間はデータ入力は0または1のいずれかに保持しなければならない。

f:id:tosh419:20160724225436p:plain

f:id:tosh419:20160724231904p:plain

トグルフリップフロップ

トグルフリップフロップの回路図を示す。Dフリップフロップの出力Qが自己のデータ自己DにNOTゲート経由で帰還されている。

f:id:tosh419:20160725203652p:plain

f:id:tosh419:20160725204627p:plain

Dフリップフロップの初期状態Q=0とすれば、Qは1となる。最初のクロックの立ち上がりで、Q=1が取り込まれ、直後にQ=1、Q=0となる。次のクロックの立ち上がりで、Q=0が取り込まれるので、直後にQ=0、Q=1となる。出力Qから出力される信号は、入力されるクロック周波数の半分の周波数となるため、この回路を２分周回路という。

上の回路は常にクロック信号の１／２の周波数の信号を生成するが、これを以下のように変更すると、制御信号T=1の間だけ１／２の周波数の信号を出力し、T=0のときは前の値を保持することができる。 f:id:tosh419:20160725205625p:plain

この回路をシンボルで書くと以下のようになる。 f:id:tosh419:20160725205806p:plain

verilogでトグルフリップフロップの記述をしてみよう。

module TFF_VERILOG(PSW0, LED0);

  input PSW0;
  output LED0;

  reg LED0;

  always @ (posed PSW0) begin 
    LED0 <= ~LED0;
  end

endmodule

クロックイネーブル

前述のDフリップフロップでは次のクロックの立ち上がりまでの期間、データの記憶が可能だが、もっと長い期間データを記憶しておくことが必要だ。そこで、次のクロックが来ても、データを更新しないような制御入力端子を追加したものが、クロックイネーブルだ。

f:id:tosh419:20160725210724p:plain

クロックイネーブル付きDフリップフロップではCE入力が0のときにはいくらエッジが来ても出力Qは変化しない。CEが1の時のクロックの立ち上がりエッジでD入力からのデータを取り込み、出力Qへ反映する。

内部回路を以下に示す。クロック入力を抑制するにはCLKにANDゲートを挿入する方法もあるが、完全同期式回路ではフリップフロップのCLKにゲートを挿入することは禁止される。

代わりに、以下の図のようにフリップフロップの入力Dの前に幾つかのゲートを挿入する。

f:id:tosh419:20160725214224p:plain

外部入力CEにより、現在のQの出力値を保持するか、外部入力Dからの値を取り込むか選択するようになっている。マルチプレクサはS0=0のとき、Q=D0、S0=1の時はQ=D1となる。以下にverilogのコードを示す。

module DFFE_VERILOG(SW0, SW1, SW2, LED0);
 
  input SW0;
  input SW1;
  input SW2;
  output LED0;
  
  reg LED0;

  always @(posedge SW0) begin
    if (SW1 == 1'b1) begin
      LED0 <= SW2;
    end
  end

endmodule

セットリセット

フリップフロップに保持されている値を強制的に1あるいは0にするための制御入力がそれぞれセット、リセットである。Dフリップフロップを例にセット入力端子Sとリセット入力端子Rを追加した回路シンボルと内部回路を以下に示す。

f:id:tosh419:20160725220003p:plain

verilogのコードを以下に示す。

module DFFERS_VERILOG(SW0, SW1, SW2, SW3, SW4, LED0);

  input SW0;
  input SW1;
  input SW2;
  input SW3;
  input SW4;
  output LED0;

  reg LED0;

  always @(posedge SW0) begin
    if (SW == 1'b1) begin
      LED0 <= 1'b0;
    end
    else if (SW2 == 1'b1) begin
      LED0 <= 1'b1;
    end
    else if (SW3 == 1'b1) begin
      LED0 <= SW4;
    end
  end

endmodule

クロックイネーブル/セットリセット付きトグルフリップフロップ

クロックイネーブルやセットリセットの機能についてはDフリップフロップに限られず、他のフリップフロップにも追加できる。また、クロックイネーブル機能とセットリセット機能は同時に追加できる。以下はクロックイネーブル/セットリセット付きトグルフリップフロップの回路シンボルと内部回路である。

f:id:tosh419:20160730203430p:plain

f:id:tosh419:20160730204459p:plain

verilogのコードを示す。

module TFFERS_VERILOG(SW0, SW1, SW2, SW3, LED0);

  input SW0;
  input SW1;
  input SW2;
  input SW3;
  output LED0;

  reg LED0;

  always @(posed SW0) begin
    if (SW1 == 1'b1) begin
      LED0 <= 1'b0;
    end
    else if (SW2 == 1'b1) begin
      LED0 <= 1'b1;
    else if (SW3 == 1'b1) begin
      LED0 <= ~LED0;
    end
  end

endmodule

制御端子の優先順位はリセットが最優先で、次にセット、クロックイネーブルと続き、トグル入力は最も優先順位が低くなっている。

完全同期式回路

複数のフリップフロップを用いる場合、気をつけなければならないのが、クロックスキューだ。以下の回路のようにすべての順序回路の状態変化が同時に起こる回路を完全同期式回路という。こうすることで、すべての回路の0,1の変化がクロックに同期して起こるため、１クロックを単位とした時間の概念を回路設計に取り入れることができる。

f:id:tosh419:20160730210235p:plain

２つのDフリップフロップの例

以下に２つのDフリップフロップを直列接続した回路を示す。

D1に入力される信号は１クロック遅れてD2に入力され、さらに１クロック遅れた信号がQ2から出力される。 D1に入力されるパルスは２番めのパルスの立ち上がりで最初のDフリップフロップに取り込まれる。FD1の出力であるD2は直後に１を立ち上がる。この時後段のフリップフロップは２番めのクロックの立ち上がりで、D2の状態を取り込むが、このとき　D2はまだ0であるため、FD2には０が取り込まれ、出力Q２は０のままだ。 FD2に１が取り込まれるのは３番めのクロックの立ち上がりで、３番めのクロックが立ち上がるとき、D1は０となっているので、FD1には０が取り込まれ、直後にD2は0に立ち下がる。しかし、同時にFD2がD2の状態１を取り込むので、直後に出力Q2が1となる。

ここで、注意すべきはD2の信号で、特性が同一の２つのDフリップフロップに全く同じタイミングで立ち上がるクロック信号が入力されているため、状態が変わる直前の状態が取り込まれている。

しかし、この動作が保証されるためには２つの条件があり、１つはセットアップ時間を満たしているかということ。前段のDフリップフロップの出力は必ずクロックの立ち上がりで、遷移するので、後段のDフリップフロップに入力される信号は１つ前のクロックの立ち上がりから、遷移するまでの遅れ時間TCKO経過してから確定している。

もう一つはホールド時間を満たしているかということで、前段のDフリップフロップの出力は、クロックの立ち上がりから、状態遷移するまでに遅れ時間がある。この遅れ時間が、後段のDフリップフロップの入力のホールド時間より長くなければならない。

FPGAにはクロック供給用にスキューが小さくなるように設計されたグローバルラインと呼ばれる専用配線がある。XilinxのFPGAではBUFGというプリミティブで使用できる。また、外部のオシレータ等をこのグローバルラインに接続するには、専用のGCLKというピンと、IBUFGというプリミティブを使用する必要がある。

カウンタ

2bitバイナリカウンタの内部回路を以下に示す。最初のトグルフリップフロップは２分周回路となり、後段のトグルフリップフロップはQ0=1の時にクロックの立ち上がりで値を反転させるので、出力Q1の信号周波数はQ0の更に1/2、つまり入力クロックの1/4の周波数となる。結果、入力をCLK、出力をQ1とした時、本回路は４分周回路となる。

f:id:tosh419:20160730213825p:plain

更にトグルフリップフロップを追加して、以下の様な回路を作ると、出力Q2はクロック信号の1/8、出力Q3は1/16の周波数となる。ここで、出力Q0をLSB、Q3をMSBとして、Q0〜Q3を4bitのデータとして捉えると、0000b〜1111bまでクロックの立ち上がりが来るごとにインクリメントしていることがわかり、このように出力が２進数となっているカウンタをバイナリカウンタという。

f:id:tosh419:20160730220846p:plain

最後に、2bitバイナリカウンタ、4bitバイナリカウンタのverilogコードを示す。

module CB2_VERILOG(CLK, Q);
  
  input CLK;
  output [1:0] Q;

  reg [1:0] Q;

  always @(posedge CLK) begin
    Q <= Q + 1'b1;
  end

endmodule

module CB4_VERILOG(CLK, R, CE, Q, TC, CEO);

  input CLK;
  input R;
  input CE;
  output [3:0] Q;
  output TC;
  output CEO;

  reg [3:0] Q;

  always @(posedge CLK) begin
    if (R == 1'b1) begin
      Q <= 4'd0;
    end
    else if (CE == 1'b1) begin
      Q <= Q + 1'b1;
    end
  end

  assign TC = &Q;
  assign CEO = &Q & CE;

endmodule

2016-07-19

FPGA入門　備忘録③　～組み合わせ回路編～

備忘録②の続き。

加算回路

半加算器

2進数の足し算は、

と書ける。これの足される数を入力A、足す数を入力B、その桁の加算結果を出力S、桁上りを出力COとして真理値表で示すと、以下のようになる。COは桁上りが生じたかどうかを表すビットである。

A	B	S	CO
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

この真理値表から回路を構成すると以下のようになる。 f:id:tosh419:20160711230333p:plain

この加算回路は下の桁からの桁上りを考慮しておらず、下からの桁上りがない最下位ビットのみにしか使えない。これを半加算器という。

全加算器

桁上りが生じたかどうかを表す出力COは2桁目以降、そのまま加算すればよい。この下からの桁上りを考慮して半加算器に、ビットの入力を追加した加算回路を全加算器と呼ぶ。以下に全加算器の真理値表と回路図を示す。

A	B	CI	S	CO
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

f:id:tosh419:20160719202925p:plain

次に、全加算器を用いた3bit加算回路の回路図を見てみよう。

f:id:tosh419:20160719205613p:plain

変数	変数の各ビット	信号名
被加数	A0 (LSB)	SW0
	A1	SW1
	A2 (MSB)	SW2
加数	B0 (LSB)	SW3
	B1	SW4
	B2 (MSB)	SW5
演算結果	S0 (LSB)	LED0
	S1	LED1
	S2 (MSB)	LED2
桁上げ出力	CO	LED3

AとBを加算し、LEDに出力する回路になっている。これをverilogで書くと、

module FA3_VERILOG(CO, S, A, B);

  input [2:0] A;
  input [2:0] B;
  output  CO;
  output [2:0] S;

  assign {CO, S} = A + B;

endmodule

assign {CO, S} = A + Bのところだが、まず左辺はCOは1bitで、Sは3bit、合計で4bitである。右辺は3bit同士の論理和で4bitになる。

減算回路

半減算器

2進数の引き算は、

と書ける。これの足される数を入力A、足す数を入力B、その桁の加算結果を出力S、桁上りを出力COとして真理値表で示すと、以下のようになる。BOは桁借りが生じたかどうかを表すビットである。

A	B	D	BO
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

この真理値表から回路を構成すると以下のようになる。 f:id:tosh419:20160719211654p:plain

この減算回路は下の桁への桁下がりを考慮しておらず、下への桁下がりがない最下位ビットのみにしか使えない。これを半減算器という。

全減算器

以下に全減算器の真理値表と回路図を示す。

A	B	BI	D	BO
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

f:id:tosh419:20160719212957p:plain

図は省略するが、加算器と同様に3bit減算回路のverilogは

module FS3_VERILOG(A, B, BO, D);
  
  input [2:0] A;
  input [2:0] B;
  output  BO;
  output [2:0] D;

  assign {BO, D} = A - B;

endmodule

と書ける。

負の数

減算結果の負の数を２進数で表す場合、最も単純なのは符号を表すビットを追加して、符号ビット＋絶対値として表す方法だ。符号ビットは正の時に0、負の時に1とする。つまり、-2dは値を3bitとすれば、1010bと表せる。3bitの絶対値に符号ビットを追加して表現した例を以下に示す。

10進数	符号なし2進数	符号付き2進数
15	1111	-
14	1110	-
13	1101	-
12	1100	-
11	1011	-
10	1010	-
9	1001	-
8	1000	-
7	0111	0111
6	0110	0110
5	0101	0101
4	0100	0100
3	0011	0011
2	0010	0010
1	0001	0001
0	0000	0000 or 1000
-1	-	1001
-2	-	1010
-3	-	1011
-4	-	1100
-5	-	1101
-6	-	1110
-7	-	1111

先ほどの3bit減算回路の演算結果出力と比べてみる。

減算結果(10進数)	出力パターン	符号付き2進数
	BO,D2,D1,D0	符号1bit,絶対値3bit
7	0111	0111
6	0110	0110
5	0101	0101
4	0100	0100
3	0011	0011
2	0010	0010
1	0001	0001
0	0000	0000 or 1000
-1	1111	1001
-2	1110	1010
-3	1101	1011
-4	1100	1100
-5	1011	1101
-6	1010	1110
-7	1001	1111

3bit減算回路の出力パターンと符号付き２進数を比較すると、減算結果が正の時は一致しており、また負の時もBOと符号ビットは一致している。つまり、減算結果が負となる時のD2,D1,D0の3bitの絶対値部分を変換すれば良い。この変換には補数を用いる。具体的には、

-まず、D0〜D2の各ビットを反転 -次に反転した3bitのDに1bを加算

のように行う。表で変換過程を示すと以下のようになる。

減算結果	出力パターン	D0〜D2を反転	さらに1を加算
(10進数)	BO, D2, D1, D0	BO, ~D2, ~D1, ~D0	BO, (~D2, ~D1, ~D0)+001b
-1	1111	1000	1001
-2	1110	1001	1010
-3	1101	1010	1011
-4	1100	1011	1100
-5	1011	1100	1101
-6	1010	1101	1110
-7	1001	1110	1111

各ビットを反転して1bを加算する回路は補数機と呼ばれており、以下の様な回路で示される。 f:id:tosh419:20160719221148p:plain

本では最後に、補数機を3bit減算器に組み合わせ符号付き2進数3bit減算回路を示している。回路図は省略するが、verilogだけ書いておく。

module FS3_SIGN_VERILOG(A, B, BO, D);
 
  input [2:0] A;
  input [2:0] B;
  output BO;
  output [2:0] D;

  wire [3:0] sub;
  
  assign sub = {1'b0, A} - {1'b0, B};
  assign BO = sub[3];
  assign D = sub[3] ? (~sub[2:0] + 1'b1) : sub[2:0];

endmodule

今回はここまで。次回は順序回路から。

2016-07-09

FPGA入門　備忘録②　～基本回路、組み合わせ回路編～

備忘録①からの続きになる。なお本では前回と今回の間にXilinxのISEのインストール方法、回路図エディタの使用方法などが記されている。

論理素子

まずは基本的なところから、VHDLとverilogの記法の違い。

名称	機能	VHDL	Verilog HDL
NOTゲート(インバータ)	論理反転	not	~
ANDゲート	論理積	and	&
ORゲート	論理和	or	\|
XORゲート	排他的論理和	xor	^
NANDゲート	否定論理積	nand	なし
NORゲート	否定論理和	nor	なし
XNORゲート	否定排他的論理和	xnor	~^

自分の目的はVerilog HDLを使いこなせるようになることなので、VHDLについては以後触れない。さて、本の中では以下の様な回路を回路図エディタ、VHDL、Verilog HDLの３種類で作成することを試みている。

f:id:tosh419:20160708234257p:plain

module INV_VERILOG(PSW0, LED0);
  input PSW0;
  output LED0;

  assign LED0 = ~PSW0;

endmodule

assign LED0 = ~PSW0;という記述の~がNOTゲートを表している。LED0が出力で、PSW0が入力で、PSW0をインバートしたものがLED0に接続されているということだ。

ANDゲート

VerilogではANDゲートを

assign Q = A & B;

と表し、VHDLでは、

Q <= A and B;

と表す。これを踏まえて、SW1とSW2の両者が入力されると、LED0が点灯するようなverilog のコードを書いてみよう。

module AND_VERILOG(SW0, SW1, LED0);
  input SW0;
  input SW1;
  output LED0;

  assign LED0 = SW0 & SW1;
endmodule

ORゲート

VerilogではORゲートを

assign Q = A | B;

と表し、VHDLでは、

Q <= A or B;

と表す。

XORゲート

VerilogではXORゲートを

assign Q = A ^ B;

と表し、VHDLでは、

Q <= A xor B;

と表す。

NANDゲート

VerilogではNANDゲートを

assign Q = ~(A & B);

と表し、VHDLでは

Q <= A band B

と表す。verilogではAとBのANDを括弧でくくりそれをNOTすることでNANDを表現している。

NORゲート

VerilogではNORゲートを

assign Q = ~(A | B);

と表し、VHDLでは

Q <= A nor B;

と表す。verilogではAとBのORを括弧でくくりそれをNOTすることでNORを表現している。

XNORゲート

VerilogではXNORゲートを

assign Q = A ~^ B;

と表し、VHDLでは

Q <= A xnor B;

と表す。

組み合わせ回路

上でも示したように、NANDゲートはANDゲートとNOTゲートを接続して作成できる。つまり、ANDゲートとNOTゲートによる組み合わせ回路といえる。NORゲートも同様にORゲートとNOTゲートの組み合わせで作成できる。では、ANDやOR、NOTゲートはどうだろう。実はこれもNANDゲートで作ることが可能だ。以下の図はそれぞれNANDゲートのみで構成したNOTゲート、　ANDゲート、ORゲートだ。

f:id:tosh419:20160709202201p:plain

また、XORはAND、OR、NOTを組み合わせれば構成できるので、NANDで置き換えることが可能だ。

f:id:tosh419:20160709204351p:plain

HDLの３つの記述方法

HDLにはいくつかの記述方法があり、回路によって記述しやすいものを使用する。記述方法は大きく３つあり、

論理演算子を組み合わせて記述する方法
テーブルを用いる方法
プリミティブを直接指定する方法

にわけられる。それぞれXOR回路を例に順に見ていく。

論理演算子を組み合わせて記述する方法

module XOR1_VERILOG(A, B, C);
  input A;
  input B;
  output C;

  assign C = ~(~A & ~(B & B)) & (~(~A & A) & B)));

endmodule

上の回路図と合わせて見ると理解できると思う。

テーブルを用いる方法

テーブルとは真理値表のことで、より複雑な論理を記述するのに向いている。テーブルの記述にはいくつかの方法があり、VHDLではwith select、case文を用いて、Verilogではassign、case文を用いて書く方法がある。まずはassignを用いて書いた場合を見てみよう。

module XOR2_VERILOG(A, B, C);
  input A;
  input B;
  output C;

   wire [1:0] Q;

  assign Q = {A, B};
  assign C = (Q == 2'b00) ? 1'b0 :
  assign C = (Q == 2'b01) ? 1'b1 :
  assign C = (Q == 2'b10) ? 1'b1 :
  assign C = (Q == 2'b11) ? 1'b0 : 1'b0;

endmodule

まずwire宣言から。これは2bit幅のバスラインQを宣言している。 assign Q = {A, B}でQの上位ビットをAに、下位ビットをBに接続している。次に、assign C = (Q==2b'00) ? 1'b0 :で、Qの値が00であれば、Cに0を出力する事を指定している。最後の1'b0はCのデフォルト値で、Qの値が未指定の場合の出力値を0としている。

次に、case文で記述したものを見てみる。

module XOR3_VERILOG(A, B, C);
  input A;
  input B;
  output C;
  
  reg C;
  
  wire [1:0] Q;

  assign Q = {A, B};

  always @(Q) begin
    case (Q)
      2'b00:  C = 1'b0;
      2'b01:  C = 1'b1;
      2'b10:  C = 1'b0;
      2'b11:  C = 1'b0;
      default:  C = 1'b0;
    endcase
  end

endmodule

Cはalways文の中で使用するので、reg C;と宣言する必要がある。always文については長くなるので後回し。

プリミティブを直接指定する方法

各デバイス特有の回路を、直接指定する際に使用する。したがって、指定できるプリミティブはデバイスによって異なる。FPGAごとに使えるライブラリのガイド一覧はXIlinxのHPで公開されている。 verilogでXOR2プリミティブを直接呼ぶ例を見てみよう。

module XOR4_VERILOG_TOP(A, B, C);
  input A;
  input B;
  output C;

  XOR2 instance1(.O(C), .IO(A), .I1(B));

endmodule

instance1という名前のXOR2に各信号を接続している。カッコ内の.O(C)という記述はXOR2の出力ピンOと外部出力ピンCが接続されることを意味する。ここの信号名OやIOなどはライブラリガイドに則った名称である必要がある。

マルチプレクサ

実用的な組み合わせ回路の一例としてマルチプレクサを取り上げる。マルチプレクサの真理値表は、

D0	D1	S0	O
0	0	0	0
0	1	0	0
1	0	0	1
1	1	0	1
0	0	1	0
0	1	1	1
1	0	1	0
1	1	1	1

f:id:tosh419:20160711213455p:plain

右図で示すようにマルチプレクサはS0が0の時はO=D0となり、1の時はO=D1となる。つまり、Oに出力するデータを、S0によって選択する回路となっている。

1bit２入力マルチプレクサの内部回路を見てみよう。 f:id:tosh419:20160711220022p:plain

S0=0の時は、D0側のANDゲートがアサート(EN)され、D1側はネゲート(Disable)される。逆に、S0=1の時はD0側のANDゲートがネゲートされ、D1側のANDゲートがアサートされる。

これは、S=1の時にスイッチが押されて、DOにDINの値が出力され、S=0の時はスイッチが切り離され、DOが0となると考えられる。verilogでは以下のように書ける。

module M2_1_VERILOG(D0, D1, S0, 0);
  
  input D0;
  input D1;
  input S0;
  output O;

  wire d0_sel;
  wire d1_sel;

  assign d0_sel = D0 & ~S0;
  assign d1_sel = D1 & S0;
  assign O = d0_sel | d1_sel;

endmodule

デコーダ(デマルチプレクサ)

マルチプレクサの対になるのが、デマルチプレクサである。デマルチプレクサは一般にデコーダとして使われることが多く、ここでは２進数のデータを１０進数に戻すバイナリデシマルデコーダを指している。 2bitバイナリデシマルデコーダの真理値表を以下に示す。

A1	A0	E	D3	D2	D1	D0
-	-	0	0	0	0	0
0	0	1	0	0	0	1
0	1	1	0	0	1	0
1	0	1	0	1	0	0
1	1	1	1	0	0	0

E=1の時、Aに入力されるバイナリコードに応じて、出力Dのいずれかが1となる。出力Dは最下位ビットから順にD0=1、D1=2、D2=3、D3=4という形で、１０進数を表している。ここで、E=0の時は入力Aに関わらず、出力D0〜D3はすべて0になる。したがって、Aで選択した出力先のDの値はEの入力値に等しくなる。Eをデータ入力、Aを制御入力と考えると、Eの出力先を切り替える回路として利用できる。これはマルチプレクサと逆の動きなので、デマルチプレクサと呼ぶ。

Eをデータ入力として、Aを制御入力として使うものがデマルチプレクサで、Aをデータ入力とし、Eは制御入力(EN端子)として使うものがデコーダとなる。

2bitバイナリデシマルデコーダの内部回路は以下のようになっている。

f:id:tosh419:20160711224309p:plain

Eをデータ入力とした時、A0及びA1で４つのANDゲートのいずれかをアサートする選択回路となっていることが分かる。verilogのコードも示す。

module D2_4E_VERILOG(A0, A1, E, D0, D1, D2, D3);
  
  input A0;
  input A1;
  input E;
  output D0;
  output D1;
  output D2;
  output D3;

  assign D0 = E & ~A0 & ~A1;
  assign D1 = E & A0 & ~A1;
  assign D2 = E & ~A0 & A1;
  assign D3 = E & A0 & A1;

endmodule